Pochopení Hybnosti: Komplexní Průvodce pro Fyziky, Inženýry i Laiky

V rozsáhlém a fascinujícím světě fyziky a inženýrství představuje koncept hybnosti jeden ze základních pilířů, na kterých stojí naše chápání pohybu a interakcí mezi objekty. Ačkoli se na první pohled může zdát jako jednoduchá myšlenka spojená s pohybujícími se tělesy, její hloubka a důsledky sahají daleko za běžnou intuici. Hybnost, často označovaná také jako moment hybnosti v lineárním kontextu, je vektorová veličina, která kvantifikuje „množství pohybu“ objektu. Zahrnuje jak hmotnost objektu, tak jeho rychlost, a proto je klíčová pro analýzu srážek, raketového pohonu, rotace a mnoha dalších jevů, které nás obklopují i ve vzdáleném vesmíru.
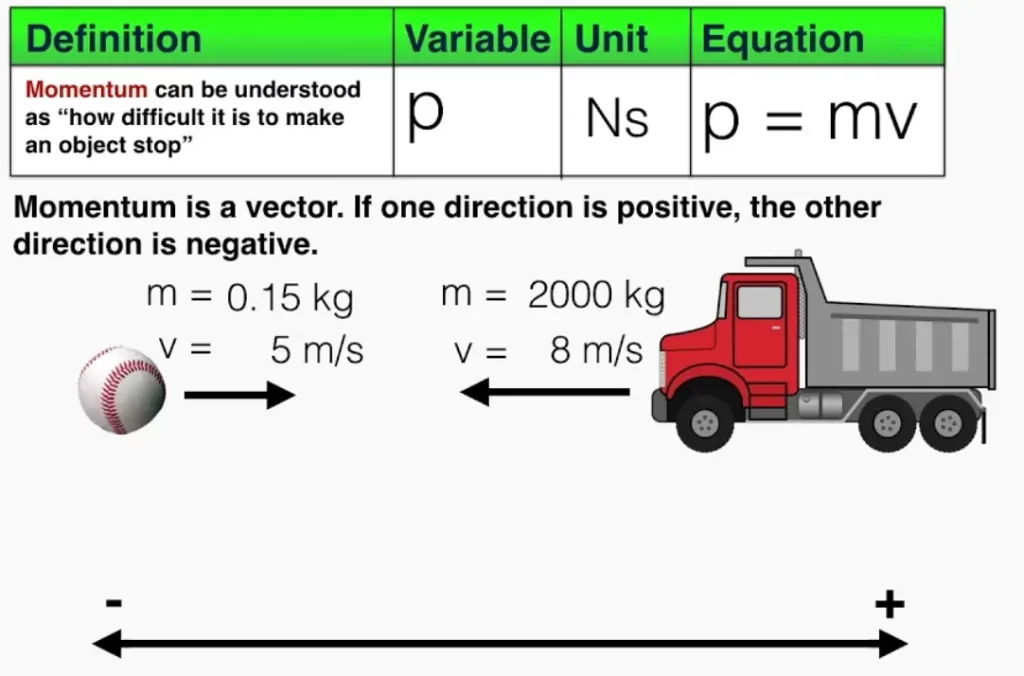
Co Přesně Je Hybnost? Definice a Základní Vzorec
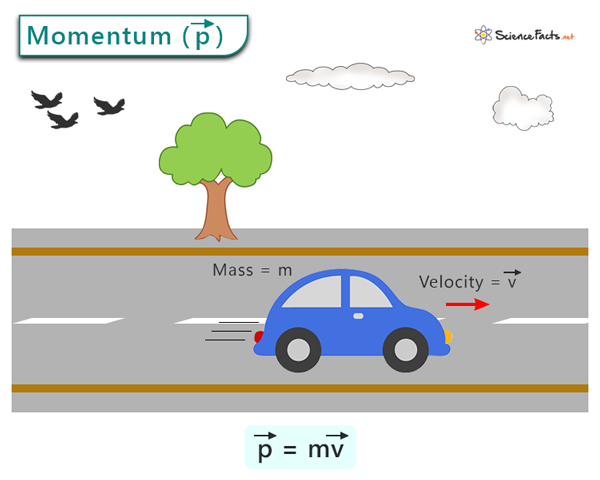
Na nejzákladnější úrovni definujeme lineární hybnost (\\vec\{p\}) objektu jako součin jeho hmotnosti (m) a jeho rychlosti (\\vec\{v\}). Matematicky to vyjadřujeme jednoduchým, ale nesmírně důležitým vzorcem:
\\vec\{p\} \= m \\vec\{v\}
Z tohoto vzorce okamžitě vyplývá několik klíčových poznatků. Za prvé, hybnost je vektorová veličina, což znamená, že má jak velikost, tak směr. Směr vektoru hybnosti je vždy stejný jako směr vektoru rychlosti. Za druhé, objekt s větší hmotností nebo vyšší rychlostí bude mít větší hybnost. To intuitivně odpovídá našim zkušenostem – těžší a rychlejší objekty je obtížnější zastavit nebo změnit jejich směr pohybu.
Jednotky Hybnosti
V soustavě SI (Système International d’Unités) se hybnost měří v jednotkách kilogram metr za sekundu (kg⋅m/s). Tato jednotka přímo vyplývá z definice hybnosti jako součinu hmotnosti (v kilogramech) a rychlosti (v metrech za sekundu).
Zákon Zachování Hybnosti: Jeden z Nejdůležitějších Principů Fyziky
Jedním z nejfundamentálnějších a nejdůležitějších principů ve fyzice je zákon zachování hybnosti. Tento zákon tvrdí, že celková hybnost izolovaného systému zůstává konstantní, pokud na něj nepůsobí žádné vnější síly. To znamená, že hybnost se v rámci systému může přerozdělovat mezi jednotlivé objekty, ale celková hybnost systému se nemění.
Matematicky můžeme tento zákon vyjádřit pro systém skládající se z více částic. Před interakcí (například srážkou) je celková hybnost systému dána součtem hybností všech částic:
\\vec\{p\}\_\{celk, před\} \= \\vec\{p\}\_\{1, před\} \+ \\vec\{p\}\_\{2, před\} \+ \.\.\. \+ \\vec\{p\}\_\{n, před\}
Po interakci je celková hybnost systému dána součtem hybností všech částic po interakci:
\\vec\{p\}\_\{celk, po\} \= \\vec\{p\}\_\{1, po\} \+ \\vec\{p\}\_\{2, po\} \+ \.\.\. \+ \\vec\{p\}\_\{n, po\}
Zákon zachování hybnosti pak říká, že pro izolovaný systém platí:
\\vec\{p\}\_\{celk, před\} \= \\vec\{p\}\_\{celk, po\}
Tento zákon má nesmírné důsledky a je klíčový pro pochopení mnoha fyzikálních jevů, od srážek atomových částic až po pohyb galaxií.
Důležitost Izolovaného Systému
Je důležité zdůraznit, že zákon zachování hybnosti platí pouze pro izolované systémy. Izolovaný systém je takový systém, na který nepůsobí žádné vnější síly. V reálném světě je dokonalá izolace obtížně dosažitelná, ale v mnoha případech můžeme systémy považovat za přibližně izolované po krátkou dobu trvání interakce (například během srážky dvou kulečníkových koulí, kde vnější síly jako tření a odpor vzduchu mohou být v porovnání s interakčními silami zanedbatelné).
Impuls Síly: Změna Hybnosti v Čase
Koncept impulsu síly úzce souvisí s hybností a poskytuje nám způsob, jak analyzovat, jak síly ovlivňují hybnost objektů. Impuls síly (\\vec\{J\}) je definován jako součin síly (\\vec\{F\}) působící na objekt a doby (\\Delta t), po kterou tato síla působí:
\\vec\{J\} \= \\vec\{F\} \\Delta t
Impuls síly je také vektorová veličina a má stejný směr jako působící síla. Jednotkou impulsu síly v SI je newton sekunda (N⋅s), což je ekvivalentní kilogram metru za sekundu (kg⋅m/s), tedy jednotce hybnosti.
Vztah Mezi Impulsem a Hybností: Věta o Impulsu a Hybnosti
Klíčový vztah mezi impulsem a hybností je dán větou o impulsu a hybnosti. Tato věta říká, že změna hybnosti objektu je rovna impulsu síly, která na něj působila:
\\Delta \\vec\{p\} \= \\vec\{p\}\_f \- \\vec\{p\}\_i \= \\vec\{J\} \= \\vec\{F\} \\Delta t
Kde \\vec\{p\}\_i je počáteční hybnost a \\vec\{p\}\_f je konečná hybnost objektu. Tato věta je přímým důsledkem druhého Newtonova pohybového zákona (\\vec\{F\} \= m \\vec\{a\}), protože z definice zrychlení (\\vec\{a\} \= \\frac\{\\Delta \\vec\{v\}\}\{\\Delta t\}) dostáváme \\vec\{F\} \= m \\frac\{\\Delta \\vec\{v\}\}\{\\Delta t\} \= \\frac\{\\Delta \(m \\vec\{v\}\)\}\{\\Delta t\} \= \\frac\{\\Delta \\vec\{p\}\}\{\\Delta t\}, a tedy \\vec\{F\} \\Delta t \= \\Delta \\vec\{p\}.
Věta o impulsu a hybnosti je nesmírně užitečná pro analýzu situací, kde na objekty působí síly po určitou dobu, například při nárazech, explozích nebo pohonu raket.
Aplikace Hybnosti v Reálném Světě: Od Sportu po Kosmické Lety
Koncept hybnosti a zákony s ní spojené mají širokou škálu aplikací v různých oblastech lidské činnosti a přírodních jevů. Některé z nejvýznamnějších aplikací zahrnují:
Sport
V mnoha sportech hraje hybnost klíčovou roli. Například v baseballu hybnost pálky a letícího míčku určuje rychlost a dráhu odpalu. V fotbalu hybnost nohy fotbalisty při kopu ovlivňuje rychlost a dostřel míče. V kulečníku a biliáru se zákon zachování hybnosti a princip impulsu síly používají k předvídání pohybu koulí po srážkách. Dokonce i v bojových uměních je pochopení hybnosti těla a úderů zásadní pro efektivní techniky.

Doprava a Bezpečnost

V oblasti dopravy je pochopení hybnosti zásadní pro zajištění bezpečnosti. Při automobilových nehodách hraje hybnost vozidel klíčovou roli v rozsahu poškození a zranění. Bezpečnostní prvky, jako jsou airbagy a bezpečnostní pásy, fungují na principu prodloužení doby působení síly při nárazu, čímž se snižuje velikost působící síly (protože impuls síly, a tedy změna hybnosti, je stejný, ale delší časový interval znamená menší sílu). V letectví a námořní dopravě je hybnost důležitá pro řízení pohybu a stability plavidel a letadel.
Raketový Pohon
Princip raketového pohonu je přímým důsledkem zákona zachování hybnosti. Raketa urychluje horké plyny (produkty hoření paliva) směrem dolů (nebo dozadu). Aby se zachovala celková hybnost systému (raketa + výfukové plyny), musí raketa získat hybnost opačným směrem, tedy směrem nahoru (nebo dopředu). Čím větší je rychlost a hmotnost vyvržených plynů, tím větší je tah rakety.
Průmysl a Výroba
V průmyslu se koncept hybnosti využívá v různých aplikacích, například při navrhování strojů a zařízení, které zahrnují nárazy nebo rázy. Pochopení sil a impulsů je důležité pro minimalizaci opotřebení a poškození strojů. Například při kování nebo lisování se využívá velká hybnost nástrojů k deformaci materiálu.
Mikroskopický Svět
Zákon zachování hybnosti platí i v mikroskopickém světě atomů a subatomárních částic. Při srážkách částic v urychlovačích se tento zákon používá k analýze výsledků experimentů a k pochopení fundamentálních interakcí.
Astronomie a Kosmologie
Na obrovských škálách vesmíru hraje hybnost klíčovou roli v dynamice planetárních systémů, galaxií a kup galaxií. Gravitační interakce mezi tělesy způsobují výměnu hybnosti, což ovlivňuje jejich dráhy a pohyby. Například slapové síly mezi Zemí a Měsícem vedou k postupnému zpomalování rotace Země a vzdalování Měsíce, což je proces, při kterém se zachovává celkový moment hybnosti systému Země-Měsíc.
Různé Druhy Srážek a Hybnost
Srážky jsou vynikajícím příkladem aplikace zákona zachování hybnosti. V závislosti na tom, zda se kinetická energie systému během srážky zachovává, rozlišujeme dva základní typy srážek:
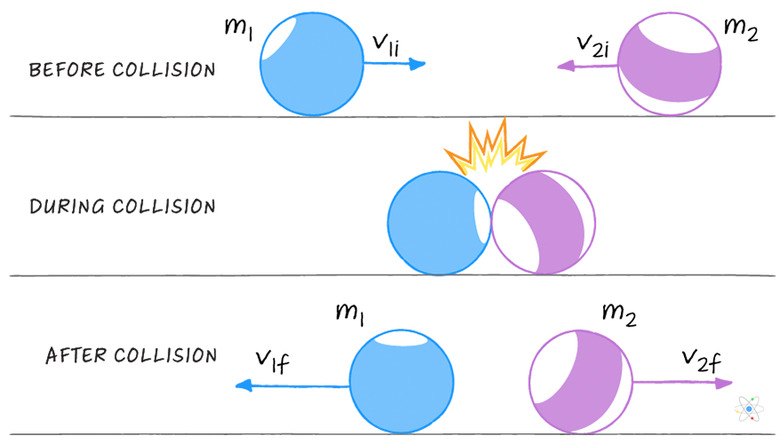
Pružné Srážky
Pružná srážka je taková srážka, při které se zachovává jak celková hybnost systému, tak celková kinetická energie systému. V ideálním případě se žádná kinetická energie nepřeměňuje na jiné formy energie, jako je teplo nebo zvuk. Příklady pružných srážek na makroskopické úrovni jsou poměrně vzácné, ale dobrým přiblížením jsou srážky velmi tvrdých elastických předmětů, jako jsou ocelové koule. Na mikroskopické úrovni jsou srážky atomů a molekul často považovány za pružné.
Pro pružnou srážku dvou těles s hmotnostmi m\_1 a m\_2 a počátečními rychlostmi \\vec\{v\}\_\{1i\} a \\vec\{v\}\_\{2i\} a konečnými rychlostmi \\vec\{v\}\_\{1f\} a \\vec\{v\}\_\{2f\} platí dva zákony zachování:
Zachování hybnosti:
m\_1 \\vec\{v\}\_\{1i\} \+ m\_2 \\vec\{v\}\_\{2i\} \= m\_1 \\vec\{v\}\_\{1f\} \+ m\_2 \\vec\{v\}\_\{2f\}
Zachování kinetické energie:
\\frac\{1\}\{2\} m\_1 v\_\{1i\}^2 \+ \\frac\{1\}\{2\} m\_2 v\_\{2i\}^2 \= \\frac\{1\}\{2\} m\_1 v\_\{1f\}^2 \+ \\frac\{1\}\{2\} m\_2 v\_\{2f\}^2
Nepružné Srážky
Nepružná srážka je taková srážka, při které se celková hybnost systému zachovává, ale celková kinetická energie systému se nezachovává. Část kinetické energie se přeměňuje na jiné formy energie, jako je teplo, zvuk nebo deformační práce. Většina srážek v reálném světě je do určité míry nepružná.
Zvláštním případem nepružné srážky je dokonale nepružná srážka, při které se srážející se objekty po srážce spojí a pohybují se společnou rychlostí. V tomto případě je ztráta kinetické energie maximální (vzhledem k zachování hybnosti).
Pro nepružnou srážku dvou těles platí pouze zákon zachování hybnosti:
m\_1 \\vec\{v\}\_\{1i\} \+ m\_2 \\vec\{v\}\_\{2i\} \= m\_1 \\vec\{v\}\_\{1f\} \+ m\_2 \\vec\{v\}\_\{2f\}
Kinetická energie se nezachovává, takže:
$\frac{1}{2} m_1 v_{1i}^2 + \frac{1}{2} m_2 v_{2i}^2 \neq \frac{1}{





